Absolute direction of bias/indirectness • triangulate

Absolute directions of bias/indirectness

The first step of the adjustment is to calculate the absolute direction of bias/indirectness. A helpful way to understand this. plotted on a standard forest plot. Note that the red arrows show the absolute direction of bias, not the direction of adjustment.

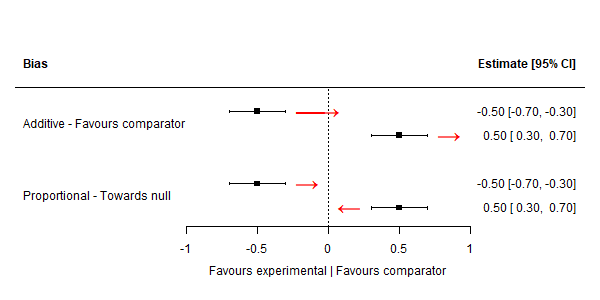
For additive bias/indirectness, the position of the point estimate does not effect the absolute direction of bias. That is, regardless of whether the point estimate is above or below the null, the absolute direction of bias/indirectness will be the same.

In contrast, for proportional bias/indirectness, the absolute direction of bias depends on the position of the effect estimate. There are two scenarios to consider:

Point estimate below NULL

If the effect estimate is below the null, then bias towards the null would be adjusted for by moving the effect estimate proportionally to the left. Conversely, bias away from the null would be adjusted for moving the point estimate proportionally to the right.

Point estimate above NULL - Bias towards the NULL

In contrast, if the effect estimate is below the null, then bias towards the null would be adjusted for by moving the effect estimate proportionally to the left. Conversely, bias away from the null would be adjusted for moving the point estimate proportionally to the right.

For example, if the effect estimate represents a protective effect (below the null), then bias towards the null would be adjusted for by moving the effect estimate proportionally to the right. In contrast, if the effect of the intervention is harmful (effect estimate above the null), bias towards the null would be adjusted for by moving the effect estimate proportionally to the left.

Adding the adjustment values

The absolute direction is also used when defining the sign of the prior in the tri_append_*() functions. If the bias/indirectness is expected to pull the effect to the right (absolute direction = right), it is given a positive sign. This is because in tri_calculate_adjusted_estimates(), we are subtracting the total additive bias from the effect estimate $y_i$ .

So to correct for an absolute direction to the right, we want the sign of the prior to be positive (e.g. N(0.9, 0.5)), so that when it is subtracted from the effect estimate, the overall impact is negative (and so we shift the effect estimate to the left):

$y_i - (0.6)$ = $y_i - 0.6$

Conversely, when the assessment is that the absolute direction of bias is to the left, we want the sign of the bias correction to be negative (e.g. N(-0.9, 0.5)), so that we are shifting the effect estimate to the right:

$y_i - (-0.6)$ = $y_i + 0.6$

See Section 6.1 of Turner et al. for the derivation of these equations.

Example

To illustrate this and ensure that our code is working correctly, lets consider a simple dataset of 6 studies, with each study fulfilling one of the scenarios described above.

# Create the example dataset
example_data <- tibble(
  study = paste("Study", 1:6),
  yi = c(-.2,.25, -.1,-.3,.1,.3),
  vi = round(runif(6, -.05,.05),3), 
  d1j = rep("moderate", 6),
  d1t = c(rep("add",2),rep("prop",4)),
  d1d = c("Favours comparator", "Favours experimental",
        "Away from null", "Towards null",
        "Away from null", "Towards null")
  )

# Complete the preparation steps of triangulate
example_data_prepped <- example_data %>%
  tri_to_long() %>%
  tri_absolute_direction() %>%
  tri_append_bias(dat_bias_values)

Additive - Favours comparator - right - positive sign

example_data[1,]
#> # A tibble: 1 × 6
#>   study      yi     vi d1j      d1t   d1d               
#>   <chr>   <dbl>  <dbl> <chr>    <chr> <chr>             
#> 1 Study 1  -0.2 -0.042 moderate add   Favours comparator
example_data_prepped[1,]
#> # A tibble: 1 × 11
#>   study     yi     vi domain j     t     d     bias_m_add bias_v_add bias_m_prop
#>   <chr>  <dbl>  <dbl> <chr>  <chr> <chr> <chr>      <dbl>      <dbl>       <dbl>
#> 1 Study…  -0.2 -0.042 d1     mode… add   right       0.09       0.05           0
#> # ℹ 1 more variable: bias_v_prop <dbl>

Additive - Favours intervention - left - negative sign

example_data[2,]
#> # A tibble: 1 × 6
#>   study      yi    vi d1j      d1t   d1d                 
#>   <chr>   <dbl> <dbl> <chr>    <chr> <chr>               
#> 1 Study 2  0.25 0.033 moderate add   Favours experimental
example_data_prepped[2,]
#> # A tibble: 1 × 11
#>   study      yi    vi domain j     t     d     bias_m_add bias_v_add bias_m_prop
#>   <chr>   <dbl> <dbl> <chr>  <chr> <chr> <chr>      <dbl>      <dbl>       <dbl>
#> 1 Study 2  0.25 0.033 d1     mode… add   left       -0.09       0.05           0
#> # ℹ 1 more variable: bias_v_prop <dbl>

Proportional - Point estimate above NULL - Towards the NULL - left - negative sign

example_data[3,]
#> # A tibble: 1 × 6
#>   study      yi    vi d1j      d1t   d1d           
#>   <chr>   <dbl> <dbl> <chr>    <chr> <chr>         
#> 1 Study 3  -0.1  0.01 moderate prop  Away from null
example_data_prepped[3,]
#> # A tibble: 1 × 11
#>   study      yi    vi domain j     t     d     bias_m_add bias_v_add bias_m_prop
#>   <chr>   <dbl> <dbl> <chr>  <chr> <chr> <chr>      <dbl>      <dbl>       <dbl>
#> 1 Study 3  -0.1  0.01 d1     mode… prop  left           0          0       -0.03
#> # ℹ 1 more variable: bias_v_prop <dbl>

Proportional - Point estimate below NULL - Away from NULL - right - positive sign

example_data[4,]
#> # A tibble: 1 × 6
#>   study      yi     vi d1j      d1t   d1d         
#>   <chr>   <dbl>  <dbl> <chr>    <chr> <chr>       
#> 1 Study 4  -0.3 -0.034 moderate prop  Towards null
example_data_prepped[4,]
#> # A tibble: 1 × 11
#>   study     yi     vi domain j     t     d     bias_m_add bias_v_add bias_m_prop
#>   <chr>  <dbl>  <dbl> <chr>  <chr> <chr> <chr>      <dbl>      <dbl>       <dbl>
#> 1 Study…  -0.3 -0.034 d1     mode… prop  right          0          0        0.03
#> # ℹ 1 more variable: bias_v_prop <dbl>

Proportional - Point estimate below NULL - Towards the NULL - right - positive sign

example_data[5,]
#> # A tibble: 1 × 6
#>   study      yi     vi d1j      d1t   d1d           
#>   <chr>   <dbl>  <dbl> <chr>    <chr> <chr>         
#> 1 Study 5   0.1 -0.049 moderate prop  Away from null
example_data_prepped[5,]
#> # A tibble: 1 × 11
#>   study     yi     vi domain j     t     d     bias_m_add bias_v_add bias_m_prop
#>   <chr>  <dbl>  <dbl> <chr>  <chr> <chr> <chr>      <dbl>      <dbl>       <dbl>
#> 1 Study…   0.1 -0.049 d1     mode… prop  right          0          0        0.03
#> # ℹ 1 more variable: bias_v_prop <dbl>

Proportional - Point estimate below NULL - Away from NULL - left - negative sign

example_data[6,]
#> # A tibble: 1 × 6
#>   study      yi     vi d1j      d1t   d1d         
#>   <chr>   <dbl>  <dbl> <chr>    <chr> <chr>       
#> 1 Study 6   0.3 -0.003 moderate prop  Towards null
example_data_prepped[6,]
#> # A tibble: 1 × 11
#>   study      yi    vi domain j     t     d     bias_m_add bias_v_add bias_m_prop
#>   <chr>   <dbl> <dbl> <chr>  <chr> <chr> <chr>      <dbl>      <dbl>       <dbl>
#> 1 Study 6   0.3 -3e-3 d1     mode… prop  left           0          0       -0.03
#> # ℹ 1 more variable: bias_v_prop <dbl>